计算机组成知识点 - 运算方法与运算部件

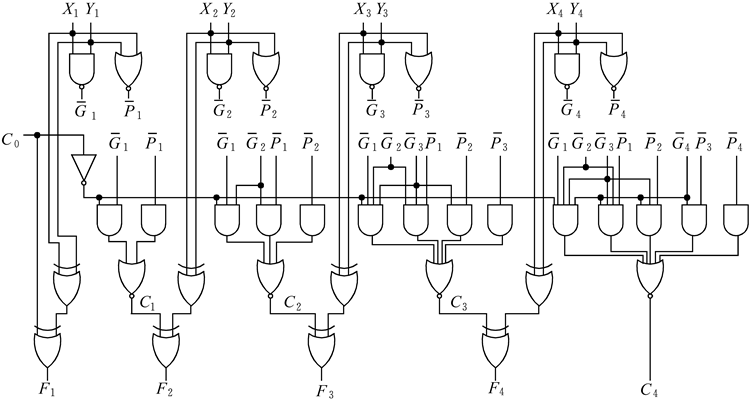
超前进位产生电路（重要）

只要满足下述两条件中任一个，就可形成C1：

1. X1,Y1均为“1”；
2. X1,Y1任一为“1”，且进位C0为“1”。

由此，可得C1的表达式为：

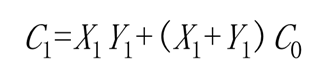
只要满足下述条件中任一个，就可形成C2：

1. X2,Y2均为“1”；
2. X2,Y2任一为“1”，且X1,Y1均为“1”；
3. X2,Y2任一为“1”，同时X1,Y1任一为“1”，且C0为“1”。

由此，可得C2的表达式为：

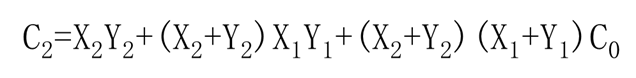
同理，可有C3，C4表达式如下：

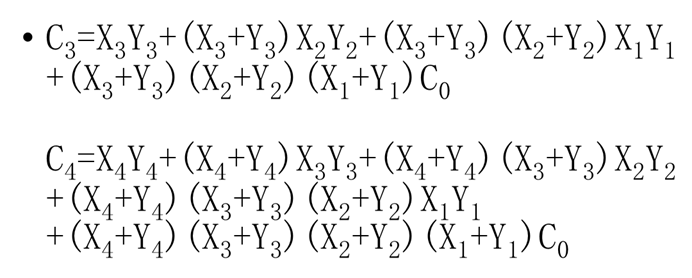
下面引入进位传递函数Pi和进位产生函数Gi：

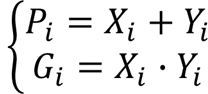
• Pi的意义是：当Xi，Yi中有一个为“1”时，若有进位输入，则本位向高位传送进位，这个进位可看成是低位进位越过本位直接向高位传递的
• Gi的意义是：当Xi，Yi均为“1”时，不管有无进位输入，定会产生向高位的进位

将Pi、Gi代入C1～C4，可得：

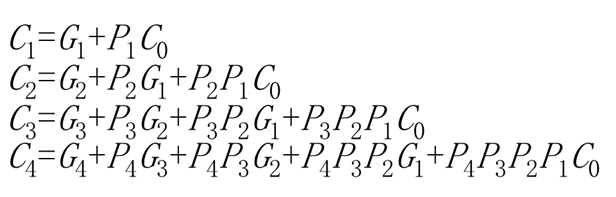
改写为：

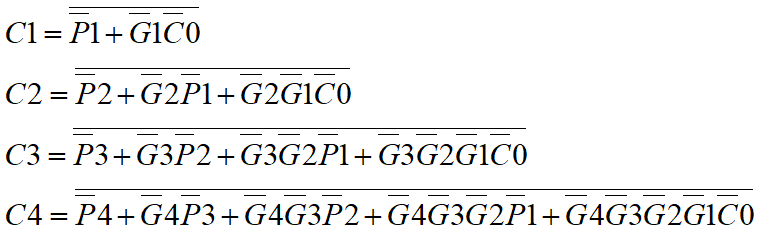
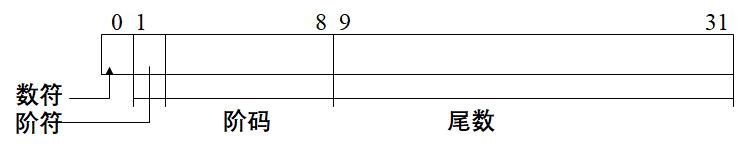
数制

• 二进制数 <=> 八进制数：3位二进制数组成1位八进制数
• 二进制数 <=> 十六进制数：4位二进制数组成1位十六进制数
  • 兼有整数和小数部分的数：对整数部分将0补在数的左侧，对小数部分将0补在数的右侧
• 八进制数 <=> 十六进制数：用二进制数作为中间媒介
• 二进制数 => 十进制数：
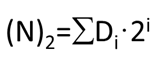
• 十进制数 => 二进制数：
  • 整数部分：除2取余数法（到商为零，倒序排列）
  • 小数部分：乘2取整数法（到小数为零或达精度，正序排列）
  • 既有整数部分，又有小数部分：分别转换后拼接

机器数

假设机器数为小数，符号位在最左面，小数点在符号位和数值之间，数的真值用X表示。

原码

反码

补码

整数的表示形式

加减法溢出判断

1. 结果的符号位变为相反时才溢出：
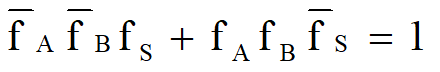
2. 数值最高位进位和符号位进位不同才溢出：
3. 双符号位（“变形补码”）：00表示结果为正，11表示结果为负；01表示“上溢”，10表示“下溢”

移码

浮点数

浮点数：指小数点位置可浮动的数据

$N=M\cdot R^E$

N是浮点数，M为尾数，E为阶码，R为阶的基数(底)

规格化浮点数

为了保证数据精度，需要对其进行规格化。

当R=2，尾数不为0时，绝对值应大于或等于0.5(十进制数)

即规格化后的浮点数具有形式：

$\plusmn 0.1bbb\cdots bb \times R ^{\plusmn E}$

若表示为补码则为：

$0.1bbb\cdots bb \times R ^{E} \\ 1.0bbb\cdots bb \times R ^{E}$

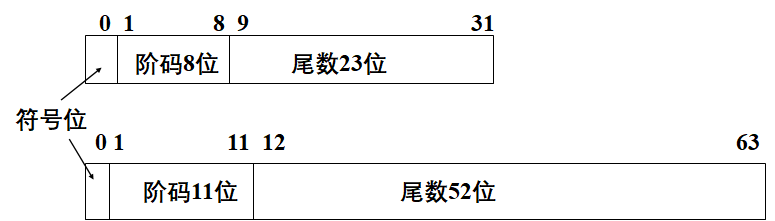
IEEE 754标准

• 单精度浮点数(32位):阶码8位，尾数24位(1位符号位)
• 双精度浮点数(64位):阶码11位，尾数53位(1位符号位)
• 阶码采用移码，尾数采用原码
• 规格化原码尾数的整数部分恒为1，在尾数中不出现，计算时自动添加上去

数值范围和精度

定点整数范围

设机器字长 n+1 位，其中符号位1位。

• 原码机器表示范围：111…1 ~ 011…1
  • 最大正数：

    $2^{n}-1$

  • 非零最小正数：1
  • 绝对值最大的负数：

    $-(2^{n}-1)$

• 补码机器表示范围：100…0 ~ 011…1
  • 最大正数：

    $2^{n}-1$

  • 最小正数：1
  • 绝对值最大的负数：100…0

    $-2^{n}$

定点小数范围

设机器字长 n+1 位，其中符号位1位。

• 原码机器表示范围：1.11…1 ~ 0.11…1
  • 最大正数：0.11…1

    $1-2^{-n}$

  • 非零最小正数：0.00…1

    $2^{-n}$

  • 绝对值最大负数：1.11…1

    $-(1-2^{-n})$

• 补码机器表示范围：100…0 ~ 011…1
  • 最大正数：0.11…1

    $2^{n}-1$

  • 非零最小正数：0.00…1

    $2^{-n}$

  • 绝对值最大负数：1.00…0 = -1

浮点数范围

设机器字长 m+n+2 位，阶码 m+1 位，其中阶符1位；尾数 n+1 位，其中数符1位（阶码基数为2），若阶码和尾数均用补码表示，说明在尾数规格化和不规格化两种情况下，它所能表示的最大正数，非零最小正数，绝对值最大的的负数，绝对值最小的负数各是哪几个数？写出机器数，并给出十进制值（不采用隐藏位）。若阶码用移码，尾数仍用补码，上述各值有变化吗？若有变化，请列出。

补码规格化

• 最大正数：阶码 011…1（m+1 位） ，尾数 0.11…1（n+1 位），真值

  $(1-2^{-n})\times 2^{2^m-1}$

• 非零最小正数：阶码 100…0（m+1 位） ，尾数 0.10…0（n+1 位），真值

  $2^{-1}\times 2^{-2^m}=2^{-(2^m+1)}$

• 绝对值最小负数：阶码 100…0（m+1 位） ，尾数 1.01…1（n+1 位），真值

  $-(2^{-1}+2^{-n})\times 2^{-2^m}$

• 绝对值最大负数：阶码 011…1（m+1 位） ，尾数 1.00…0（n+1 位），真值

  $-1\times 2^{2^m-1}$

补码非规格化

• 最大正数：阶码 011…1（m+1 位） ，尾数 0.11…1（n+1 位），真值

  $(1-2^{-n})\times 2^{2^m-1}$

• 非零最小正数：阶码 100…0（m+1 位） ，尾数 0.00…1（n+1 位），真值

  $2^{-n}\times 2^{-2^m}=2^{-(2^m+n)}$

• 绝对值最小负数：阶码 100…0（m+1 位） ，尾数 1.11…1（n+1 位），真值

  $-2^{-n}\times 2^{-2^m} = -2^{-(2^m+n)}$

• 绝对值最大负数：阶码 011…1（m+1 位） ，尾数 1.00…0（n+1 位），真值

  $-1\times 2^{2^m-1}$

阶码用移码，尾数仍用补码

• 若不考虑溢出，上述各值无变化，只是阶码符号位取反。

• 若考虑到下溢处理，若阶码

  $\leq -2^{m}$

  按下溢处理成机器零。故非零最小正数和绝对值最小负数如下表所示：

值	规格化	非规格化
非零最小正数	$$2^{-1}\times 2<sup>{-2</sup>m+1}=2<sup>{-2</sup>m}$$	$$-2^{-n}\times 2<sup>{-2</sup>m+1}=-2<sup>{-2</sup>m-n+1}$$
绝对值最小负数	$$-(2<sup>{-1}+2</sup>{-n})\times 2<sup>{-2</sup>m+1}$$	$$-2^{-n}\times 2<sup>{-2</sup>m+1}=-2<sup>{-2</sup>m-n+1}$$

浮点数精度问题

浮点数精度 x 取决于尾数中数值位的个数 n，计算公式为：

$2^n=10^x \ \Longleftrightarrow \ x=n\cdot log(2) \ , \ log(2) \approx 0.301$

定点数乘法（重要）

定点原码一位乘法

• 求得一个相加数，就与上次部分积相加
• 求本次部分积时，前一次部分积 >> 一位，同时乘数寄存器 >> 一位，接受部分积移出的位数

定点补码一位乘法

• 当乘数Y为正时，定点补码一位乘法的运算过程与定点原码一位乘法相同。
• 当乘数Y为负时，还需要补充进行加[-X]补操作。

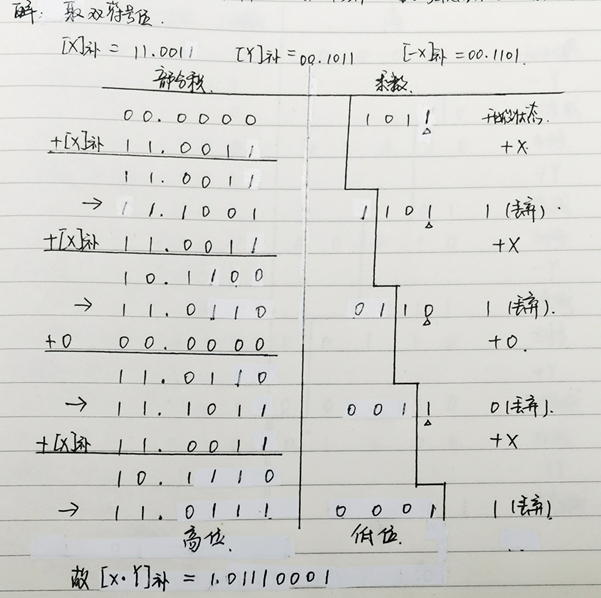
例：设X=-0.1101，Y=0.1011，求[X·Y]补，要求写出定点补码一位乘法的机器实现过程。

布斯一位乘法规则

定点数两位乘法

两位乘数有4种可能组合，对应以下操作：

• 00——相当于0•X，部分积为Pi +0，然后右移两位；
• 01——相当于1•X，部分积为Pi+X，然后右移两位；
• 10——相当于2•X，部分积为Pi+2X，然后右移两位；
• 11——相当于3•X，部分积为Pi+3X，用 (Pi - X)+4X 来替代：本次-X，然后右移两位，下次+X，不再移位。使用触发器C记录是否有欠位
• 如果最后一次操作欠下+4X，则最后一次右移2位后还需补充+X操作，+X后不再移位。

浮点数运算

加减法（重要）

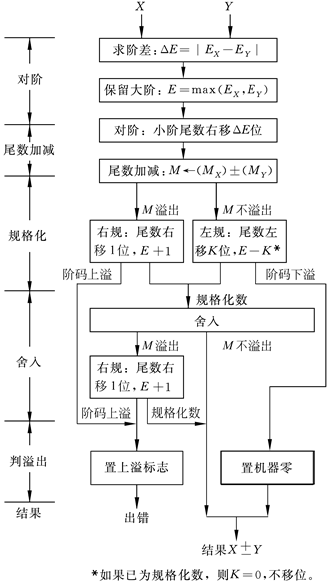
1. 对阶：dE=|Ex-Ey|；小阶向大阶看齐。（保留大阶）
2. 尾数的加（减）运算。
3. 规格化处理
   • 如果结果的两个符号位的值不同，表示运算尾数结果溢出，应“右规”，即尾数结果右移一位，阶码+1。
   • 如果最高数值位与符号位相同（不满足规格化要求），应“左规”，此时尾数连续左移，直到最高数值位与符号位的值不同为止；同时从阶码中减去移位的位数。
4. 舍入处理。0舍1入法
5. 检查是否溢出。
   • 阶码下溢：置机器零
   • 阶码上溢：置上溢标志

乘法

1. 检测操作数是否为0，若其中有一个操作数为0，则置结果为0；
2. 阶码相加，阶符相同的加可能会溢出，若溢出，则作溢出处理；
3. 尾数相乘；
4. 尾数乘积规格化，只有左规；
5. 舍入
   • 截断处理：无条件地丢掉正常尾数最低位之后的全部数值
   • 舍入处理：运算过程中保留右移中移出的若干高位的值，然而再按某种规则（0舍1入法）用这些位上的值修正尾数
6. 判溢出

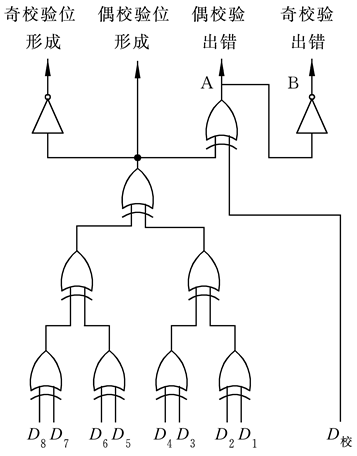
奇偶校验码

通过在数据位中加入一些冗余位，从而达到在数据传输过程中能自动发现错误（检错码）和校正错误（纠错码）

编码方法:

• 不管数据位长度多少，校验位只有一位。
• 数据位和校验位一起所含“1”的个数，只能是奇数，称为奇校验。
• 数据位和校验位一起所含“1”的个数，只能是偶数，称为偶校验。

只能发现一位错(或奇数个位错)，不能确定是哪一位错，也不能发现偶数个位错。