人工智能

December 29, 2021

人工智能与知识工程第一部分

概论

人工智能就是研究如何使一个计算机系统具有像人一样的智能特征，使其能模拟、延伸、扩展人类智能。

智能的特征：具有感知能力、具有记忆与思维能力、具有学习能力、具有行为能力

基本研究内容：知识表示、机器感知、机器思维、机器学习、机器行为

人工智能发展史

1937年，开发出世界上第一台电子计算机ABC，为人工智能的研究奠定了物质基础
1943年，M-P模型的提出，奠定了人工神经网络发展的基础。
1950年，图灵提出了著名的机器智能测试模型——图灵测试
1956年，麦卡锡(McCarthy)等10人正式提出了“人工智能” 这一术语
1982: John Hopfield 掀起神经网络的研究
1986年，Rumelhart发现了BP算法，解决了多层网的学习问题
1997: IBM 深蓝第一次击败国际象棋世界冠军
2016：AlphGo成为第一个击败人类职业棋手的软件

知识表示

状态空间法

状态：描述某类不同事物间的差别而引入的一组最少变量q0,q1,…,qn的有序集合

算符：使问题从一种状态变化为另一种状态的手段。（走步、过程、规划、数学算子、运算符号、逻辑符号等）

解题流程：

定义状态
初始状态
目标状态
列举所有可能的状态
定义算符
构建状态空间图
问题的解是由初始状态到目标状态所用算符的序列

例：从苏州大学去北京天安门的行程安排（状态空间法）（略）

产生式表示法

确定性规则知识的表示方法： P -> Q 或者 IF P THEN Q
- 三元组表示：（对象，属性，值）或（关系，对象1，对象2）
不确定性规则知识的表示方法： P -> Q （置信度）或者 IF P THEN Q （置信度）
- 四元组表示：（对象，属性，值，可信度值）或（关系，对象1，对象2 ，可信度值）

产生式系统的组成

规则库：产生式集合
综合数据库：存放输入的事实、中间的运行结果和最后结果
推理机：选择什么规则和如何应用规则
1. 匹配：将当前综合数据库的事实与规则中的条件进行比较，如果匹配则这一规则称为匹配规则
2. 冲突解决：专一性排序、规则排序、规模排序和就近排序
3. 操作：当前综合数据库将被修改

例：天气产生式系统

规则：
- R1:IF 有风，THEN 云高速移动
- R2:IF 云高速移动 AND 高温， THEN 明天天晴
综合数据库：今天有风，高温
推理：明天天气如何？
取规则R1，检查综合数据库中是否有已知事实匹配，存在“有风”这一事实，将“云高速移动”放入综合数据库中；
取规则R2，检查综合数据库中是否有已知事实匹配，存在“云高速移动”和“高温”事实，将“明天天晴”放入综合数据库中；
检查综合数据库中已经存在了“明天天晴”的事实，推出“明天天晴”的结论。

谓词逻辑法

例：下列知识是一些规则性知识：

人人爱劳动。所有整数不是偶数就是奇数。自然数都是大于零的整数。请用谓词公式表示这些知识。

解：定义谓词如下：

MAN(x): x是人。 LOVE(x,y): x爱y。

N(x): x是自然数。I(x): x是整数。

E(x): x是偶数。 O(x): x是奇数。

GZ(x): x大于零。

“人人爱劳动”用谓词公式表示为：

(\forall x)(MAN(x)\to LOVE(x,labour))

“所有整数不是偶数就是奇数”

(\forall x)(I(x)\to E(x)\vee O(x))

“自然数都是大于零的整数”

(\forall x)(N(x)\to GZ(x)\wedge I(x))

语义网络法

例：用语义网络表示下列事实：

苏州大学坐落于历史文化名城苏州，是国家“211 工程”、“2011 计划”首批入列高校。张三同志今年42岁，男性，中等身材，他工作于苏州大学。

框架表示

框架可以由框架名、槽、侧面和值四部分组成。框架一般可表示成如下格式：

<框架名>
<槽名1><侧面11><值111> …
       <侧面12><值121> …
    …
<槽名2><侧面21><值211> …
       <侧面22><值221> …
    …
<槽名n><侧面n1><值n11> …
    …
       <侧面nm><值nm1> …

确定性推理

方向

正向推理（事实驱动推理）: 已知事实 → 结论
- 简单，易实现，但目的性不强，效率低。
逆向推理（目标驱动推理）：以某个假设目标作为出发点，寻找证据。
- 主要优点：不必使用与目标无关的知识，目的性强，同时它还有利于向用户提供解释。
- 主要缺点：起始目标的选择有盲目性。
混合推理
- 先正向后逆向：先进行正向推理，帮助选择某个目标，即从已知事实演绎出部分结果，然后再用逆向推理证实该目标或提高其可信度；
- 先逆向后正向：先假设一个目标进行逆向推理，然后再利用逆向推理中得到的信息进行正向推理，以推出更多的结论
双向推理：正向推理与逆向推理同时进行，且在推理过程中的某一步骤上“碰头”的一种推理。

冲突消解策略

按针对性排序
按已知事实的新鲜性排序
按匹配度排序
按条件个数排序
按上下文限制排序
按冗余限制排序
根据领域问题的特点排序

自然演绎推理

自然演绎推理：从一组已知为真的事实出发，运用经典逻辑的推理规则推出结论的过程。

推理规则：P规则、T规则、假言推理、拒取式推理

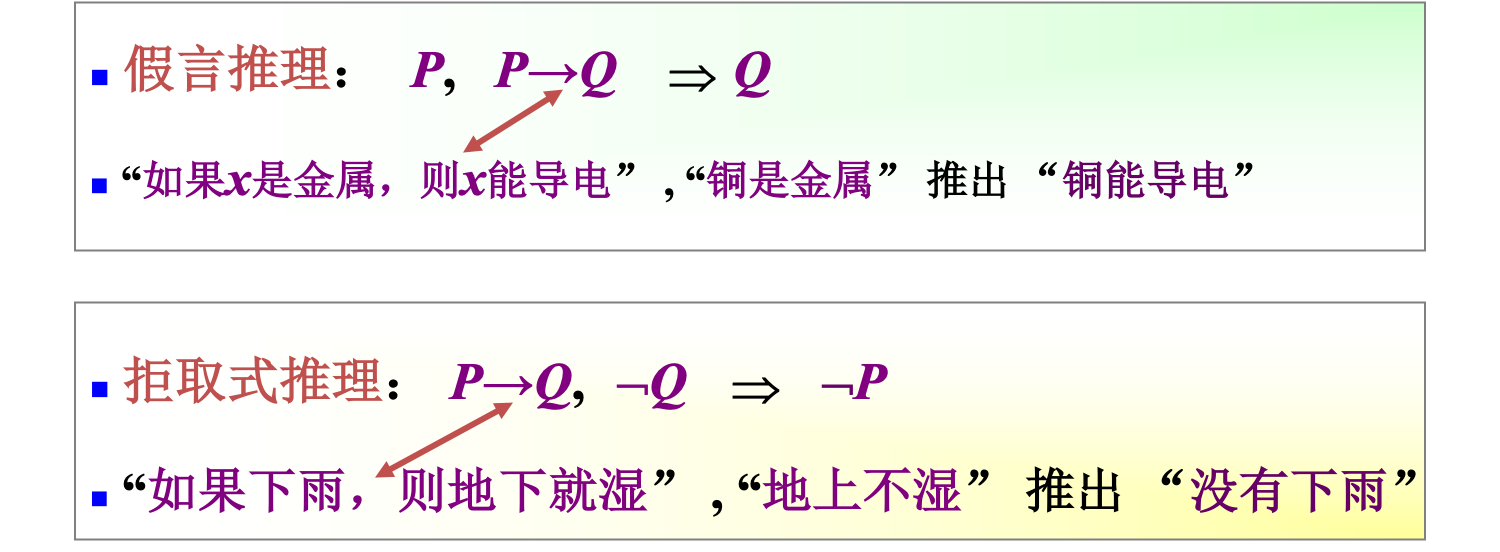
优点：

表达定理证明过程自然，易理解。
拥有丰富的推理规则，推理过程灵活。
便于嵌入领域启发式知识。

缺点：易产生组合爆炸，得到的中间结论一般呈指数形式递增。

归结反演

谓词公式化为子句集

原子（atom）谓词公式：一个不能再分解的命题。
文字（literal）：原子谓词公式及其否定。
子句（clause）：任何文字的析取式。任何文字本身也都是子句。
空子句（NIL）：不包含任何文字的子句。
子句集：由子句构成的集合。

消去谓词公式中的“->”和“<->”符号
$P \to Q \iff \neg P \vee Q$ $P \leftrightarrow Q \iff (P\wedge Q)\vee(\neg P\wedge \neg Q)$
把否定符号移到紧靠谓词的位置上
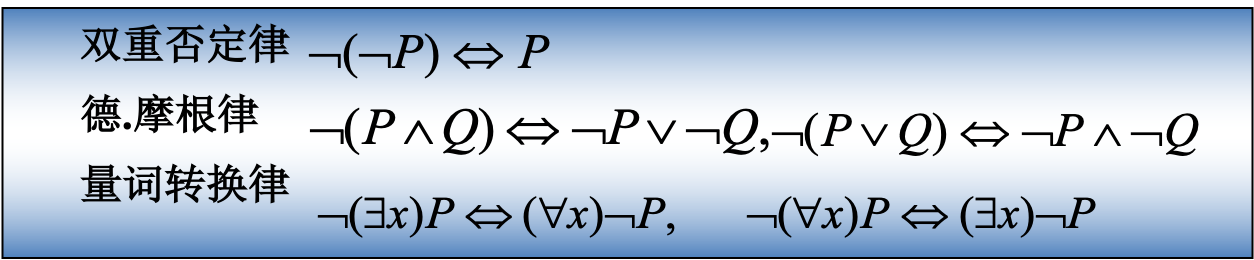
变量标准化
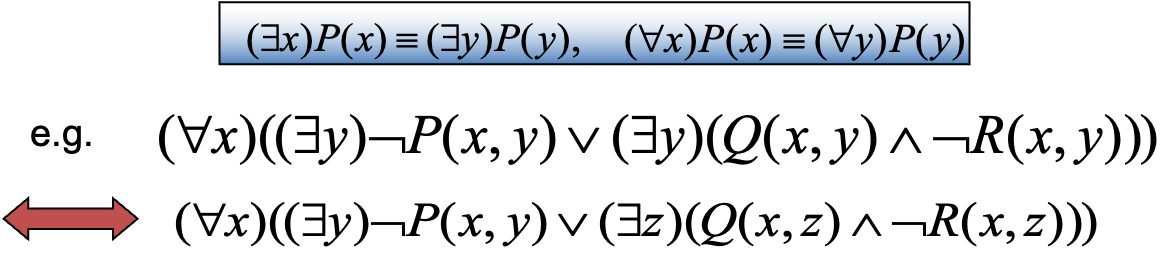
消去存在量词
1. 存在量词不出现在全称量词的辖域内。
2. 存在量词出现在一个或者多个全称量词的辖域内。
化为前束形：前束形=（前缀）{母式}
化为 Skolem 标准形
$P\vee (Q\wedge R) \iff (P\vee Q)\wedge(P\vee R)$ $P\wedge (Q\vee R) \iff (P\wedge Q)\vee(P\wedge R)$
略去全称量词
消去合取词（转换为集合）
子句变量标准化（使用不同的变量）

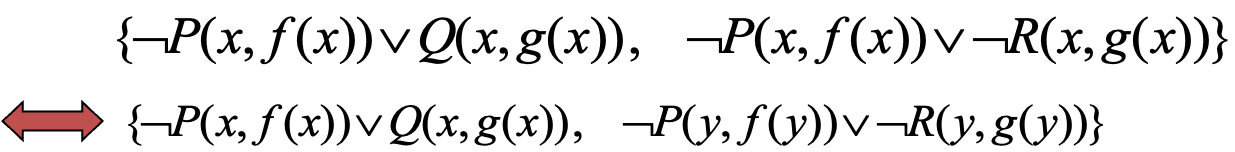
鲁滨逊归结原理

基本思想：

检查子句集 S 中是否包含空子句，若包含，则 S 不可满足。
若不包含，在 S 中选择合适的子句进行归结，一旦归结出空子句，就说明 S 是不可满足的。

若未能归结得空子句，则既不能说明 S 是可满足的，也不能说明 S 是不可满足的。

归结反演

将已知前提表示为谓词公式F。
将待证明的结论表示为谓词公式Q，并否定得到﹁ Q 。
把谓词公式集{F，﹁Q} 化为子句集S。
应用归结原理对子句集S中的子句进行归结，并把每次归结得到的归结式都并入到S中。如此反复进行，若出现了空子句，则停止归结，此时就证明了Q为真。

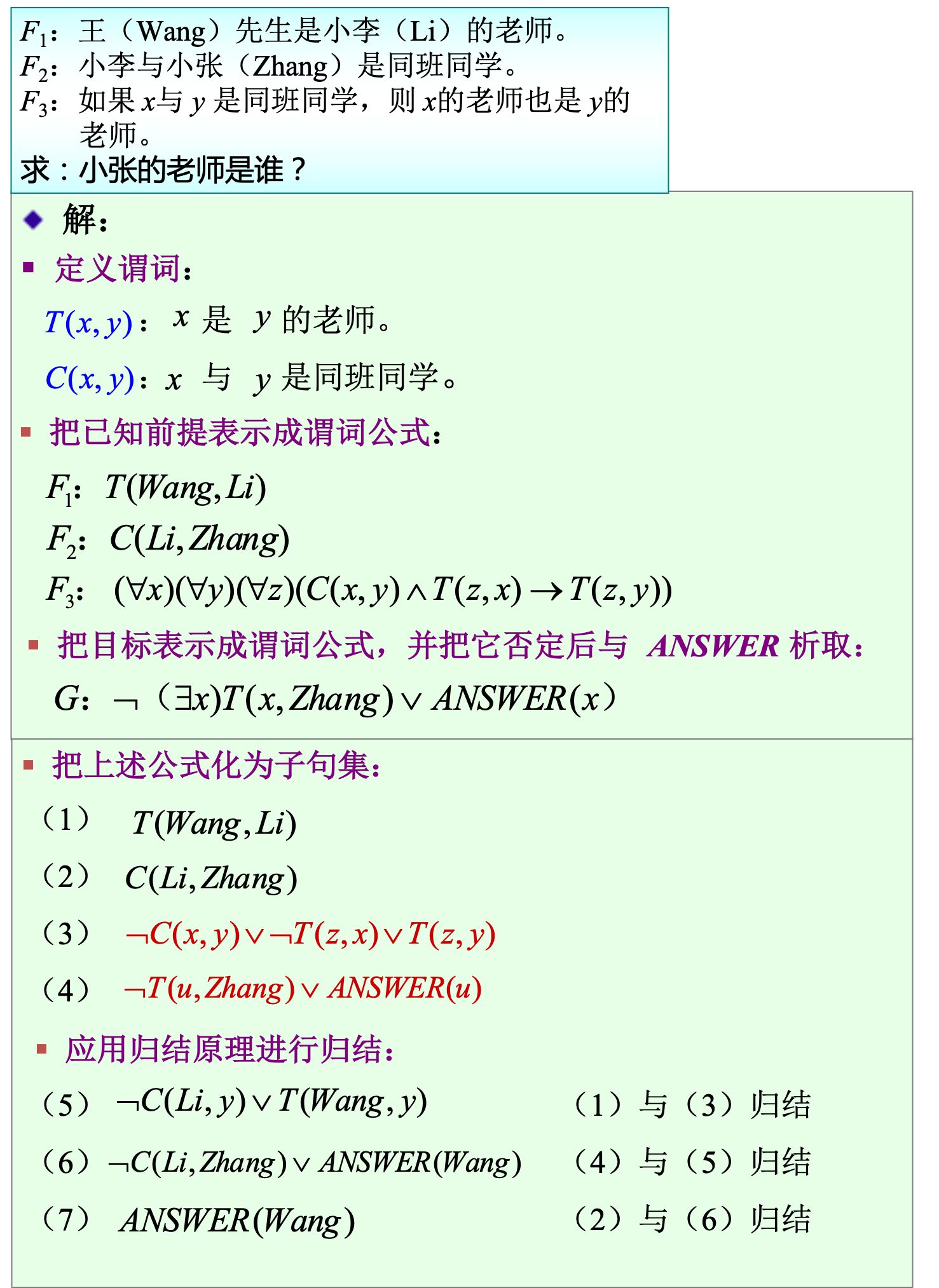
应用归结原理求解问题

已知前提 F 用谓词公式表示，并化为子句集 S ；
把待求解的问题 Q 用谓词公式表示，并否定 Q，再与 ANSWER 构成析取式（﹁ Q ∨ ANSWER ）；
把（﹁ Q ∨ ANSWER）化为子句集，并入到子句集 S中，得到子句集S’；
对子句集S’应用归结原理进行归结，若得到归结式 ANSWER ，则答案就在 ANSWER 中。

不确定性推理

可信度方法

可信度：根据经验对一个事物或现象为真的相信程度。

C-F模型：IF E THEN H (CF(H, E))

CF(H, E)：可信度因子。范围[-1, 1]，> 0 越大越支持 H 为真；< 0越小越支持 H 为假；=0无关。

静态强度 CF（H，E）：知识的强度，即当 E 所对应的证据为真时对 H 的影响程度。
动态强度 CF（E）：证据 E 当前的不确定性程度。

组合证据：合取（AND）取min，析取（OR）取max

传递算法：

CF(H)= CF(H, E) \times \max (0, CF(E))

合成算法:

证据理论

概率分配函数：把D的任意一个子集A都映射为[0，1]上的一个数M(A)。

信任函数（为真信任度）：Bel(A)为A的所有非空子集B的M(B)之和。

似然函数（非假信任度）：

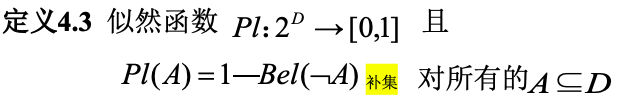
证据组合：概率分配函数的正交和

基于证据理论的不确定性推理的步骤：

建立问题的样本空间D。
由经验（题目）给出基本概率分配函数M。

利用传递算法：
$CF(H)= CF(H, E) \times \max (0, CF(E))$
以及合成算法。
计算所关心的子集A的信任函数值Bel(A)、似然函数值Pl(A)。
得出结论为真信任度：Bel(A)，非假信任度：Pl(A)。

模糊推理

模糊逻辑给集合中每一个元素赋予一个介于0和1之间的实数，描述其属于一个集合的强度，该实数称为元素属于一个集合的隶属度。集合中所有元素的隶属度全体构成集合的隶属函数。

运算：

模糊关系：

模糊关系的合成：

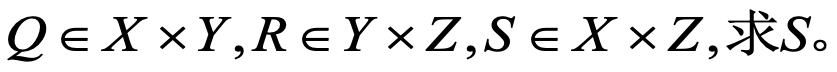
最大-最小合成：乘积取小，求和取大
最大-代数合成：乘积代数运算，求和取大

模糊推理：已知 A->B，给定输入A’，计算：

R = A^T \circ B

B' = A' \circ R

决策：

最大隶属度法
加权平均判决法：
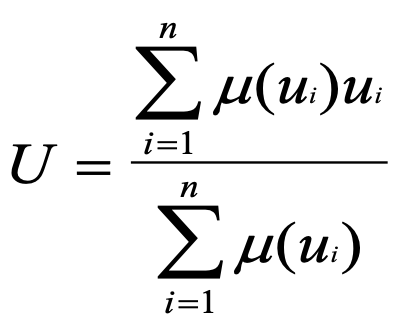
中位数法：

搜索

搜索：根据问题的实际情况，按照一定的策略或规则，从知识库中寻找可利用的知识，从而构造出一条使问题获得解决的推理路线的过程。

图搜索策略：

将问题的初始状态（状态空间图中的初始节点）当作当前节点，选择一适当的算符作用于当前状态，生成一组后继状态（或后继节点）。
检查这组后继状态中有没有目标状态，如果有，则说明搜索成功，从初始状态到目标状态的一系列算符即是问题的解。
若没有，则按照某种控制策略从已生成的状态中再选择一个状态作为当前状态。
重复上述过程，直到目标状态出现或不再有可供操作的状态及算符时为止。

盲目搜索

特点：

搜索线路是事先决定好的，没有利用被求解问题的任何信息。
在决定要被扩展的节点时，没有考虑节点是否可能出现在解的路径上。
没有考虑它是否有利于问题的求解以及所求的解是否为最优解。

宽度优先搜索：搜索是以接近起始节点的程度来依次扩展节点。搜索是逐层进行的，在对下一层的任意节点进行搜索之前，必须搜索完本层的所有节点。

深度优先搜索：先扩展最新产生的节点，深度相等的节点可以任意排列。

为了避免考虑太长的路径，往往给出一个节点扩展的最大深度——深度界限。达到深度界限，认为没有后继节点。

启发式搜索

启发式搜索（有信息搜索）：找到一种方法用于排列待扩展节点的顺序，即选择最有希望的节点加以扩展，搜索效率将会大大提高。

估价函数：从初始节点经过节点x到达目标节点的最小代价路径的代价估算值。

f(x)=g(x)+h(x)

g(x)从初始节点S₀到节点x已实际付出的代价；
h(x)从节点x到目标节点S_g的最优路径的估价代价。

g(x)的比重越大，搜索方向倾向于广度优先搜索；h(x)的比重越大，越倾向于深度优先搜索。

A*算法：

将开始节点放入Open(开始节点的F和G值都视为0);
作如下循环
1. 在Open表中查找具有最小F值的节点,并把查找到的节点作为当前节点;
2. 把当前节点从Open表删除, 加入到Closed表;
3. 对当前节点相邻的每一个节点依次执行以下步骤：
  1. 如果该相邻节点不可通行或者该相邻节点已经在Closed表中,则什么操作也不执行,继续检验下一个节点;
  2. 如果该相邻节点不在Open表中,则将该节点添加到Open表中, 并将该相邻节点的父节点设为当前节点,同时保存该相邻节点的G和F值;
  3. 如果该相邻节点在开放列表中, 则判断若经由当前节点到达该相邻节点的G值是否小于原来保存的G值,若小于,则将该相邻节点的父节点设为当前节点,并重新设置该相邻节点的G和F值.
循环结束条件：
- 当终点节点被加入到开放列表作为待检验节点时, 表示路径被找到,此时应终止循环;
- 或者当开放列表为空,表明已无可以添加的新节点,而已检验的节点中没有终点节点则意味着路径无法被找到,此时也结束循环
从终点节点开始沿父节点遍历, 并保存整个遍历到的节点坐标,遍历所得的节点就是最后得到的路径。

可采纳性：指对于可求解的状态空间图（即从状态空间图的初始节点到目标节点有路径存在）来说，如果一个搜索算法能在有限步内终止，并且能找到最优解。
单调性：在A*算法中，如果对其估价函数中的h(x)部分，加以适当的单调性限制，就可以使它对所扩展的节点的估价函数值单调递增，从而减少对OPEN表或CLOSED表的检查和调整，提高搜索效率。
信息性：A*算法的搜索效率主要取决于启发函数h(x),h(x)携带信息的多少。

About this Post

This post is written by Holger, licensed under CC BY-NC 4.0.

#机器学习 #人工智能 #考试不挂科

人工智能与知识工程第一部分

概论

人工智能发展史

知识表示

状态空间法