数字电路(第二部分:时序电路)
触发器种类总结
RS触发器
【重要】
- 特性方程:
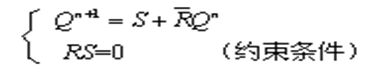
- 驱动表:
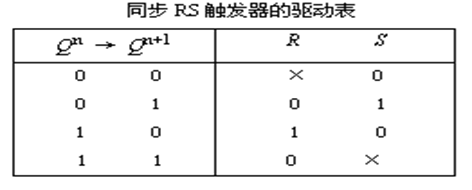
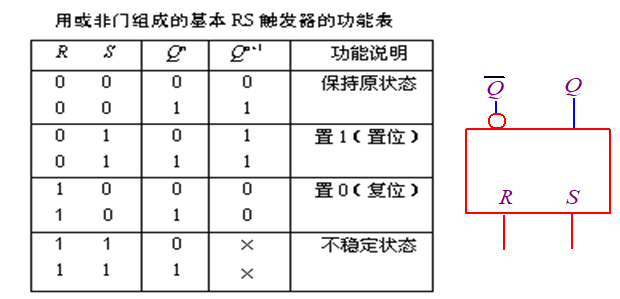
基本RS触发器
- 有两个互补的输出端,有两个稳定的状态。
- 有复位(Q=0)、置位(Q=1)、保持原状态三种功能。
- R为复位输入端,S为置位输入端,可以是低电平有效,也可以是高电平有效,取决于触发器的结构。
- 由于反馈线的存在,无论是复位还是置位,有效信号只需要作用很短的一段时间,即“一触即发”。
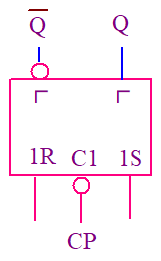
同步RS触发器
给触发器加一个时钟控制端CP,只有在CP端上出现时钟脉冲时,触发器的状态才能变化。
同步RS触发器的状态转换分别由R、S和CP控制,其中,R、S控制状态转换的方向;CP控制状态转换的时刻(上升沿-CP高有效 or 下降沿-CP低有效)。
问题:空翻 在一个时钟脉冲周期中,触发器发生多次翻转的现象
主从RS触发器
特点:
- 主从触发器的翻转是在CP由1变0时刻(CP下降沿)发生的。
- CP一旦变为0后,主触发器被封锁,其状态不再受R、S影响,因此不会有空翻现象。
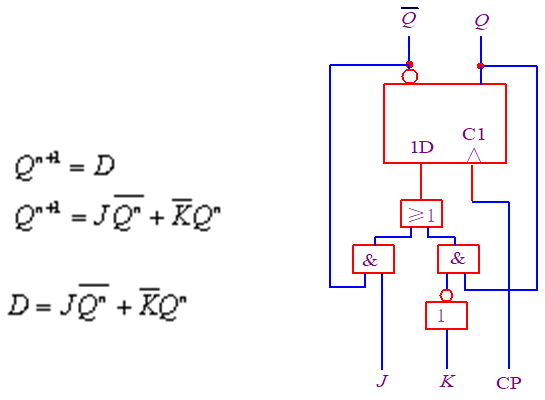
JK触发器 【重要】
- 特性方程:
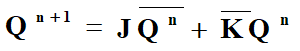
- 驱动表:
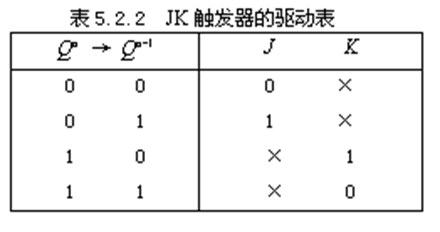
D触发器 【重要】
特性方程: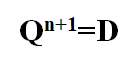
T触发器
特性方程:
T’触发器
特性方程:Q*=非Q
触发器的转换
将两种触发器的特性方程进行比较,得出结果。
JK->D

JK->T T’
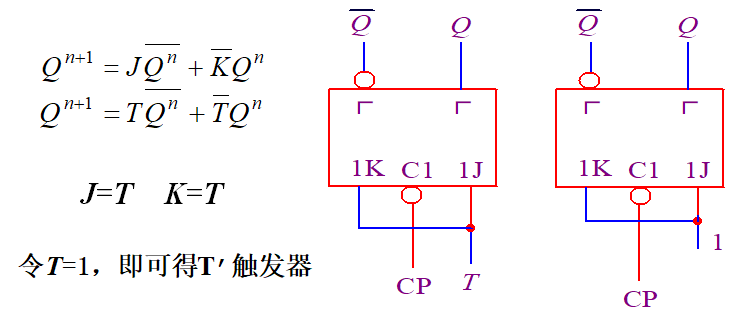
D->JK
其他之间互转
将状态转换图写成卡诺图的形式,然后求特性方程;将两种触发器的特性方程进行比较,得出结果。
时序逻辑电路
时序逻辑电路:任何一个时刻的输出状态不仅取决于当时的输入信号,还与电路的原状态有关。
- 输出方程(输出函数)
- 驱动方程(激励函数)(与触发器输入相连)
- 状态方程
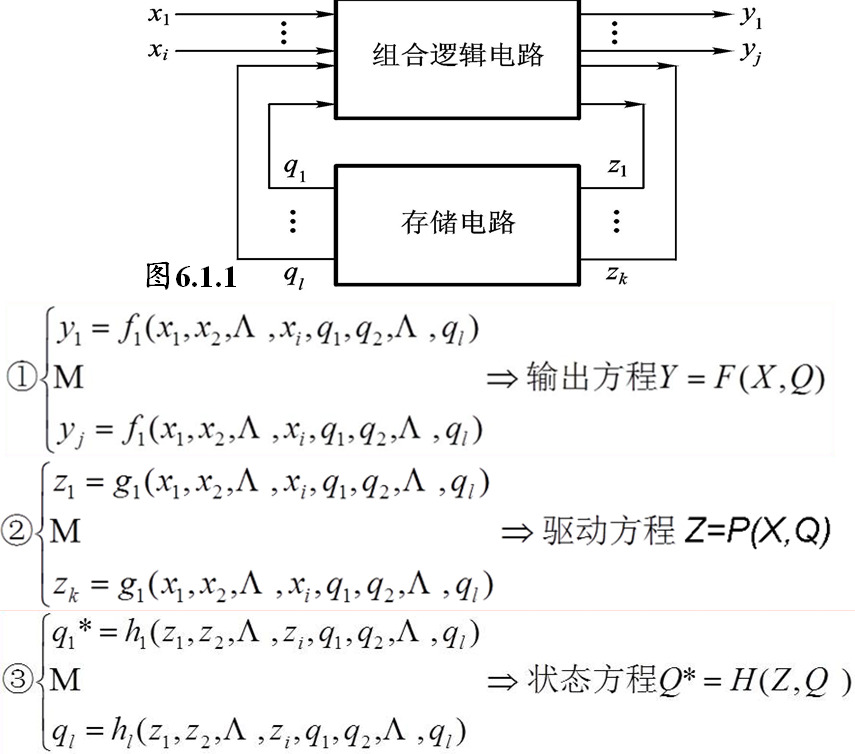
根据输出信号的特点时序逻辑电路可分为米利(Mealy)型和穆尔(Moore)型。
- Mealy类型与输入、现态有关
- Moore类型仅于现态有关
分析 【重要】
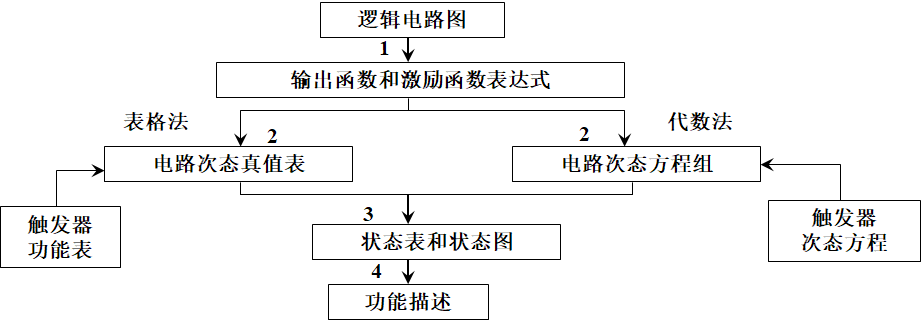
- 写出输出方程,驱动方程;
- 将驱动方程代入触发器的特性方程中,得出电路的状态方程;
- 画出状态转换表,状态转换图;
- 画出时序图(不必要);
- 分析逻辑功能。
同步时序逻辑电路的设计 【重要】

- 根据设计要求,设定状态,画出状态转换图;
- 状态分配,列状态转换编码表;
- 画出电路的次态卡诺图;由触发器的驱动表得各触发器的驱动卡诺图,再画出输出卡诺图,求各触发器的驱动方程和输出方程;
- 如果状态个数不为2^n,将驱动方程代入触发器的特性方程中,得出电路的状态方程,检查能否自启动(无关项能否进入有效状态)(如果不能,重新设计状态转换图);
- 画出逻辑电路图。
建立原始状态图和状态表
- 确定电路模型:Mealy型 or Moore型;
- 设立初始状态;
- 从初始状态出发,逐个增加和完善,并确定各时刻电路的输出。
- Mealy型:
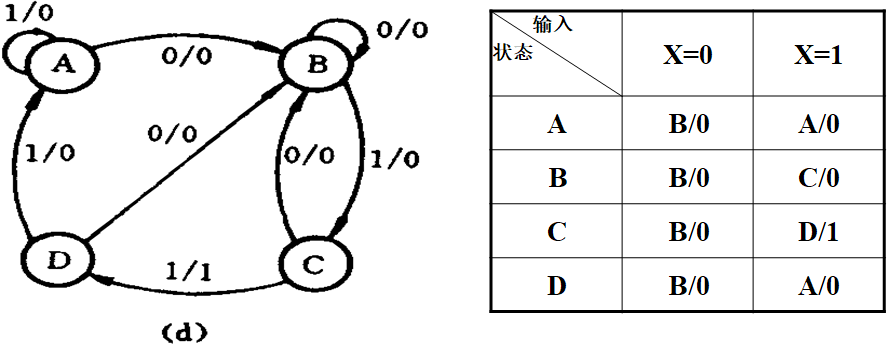
- Moore型:
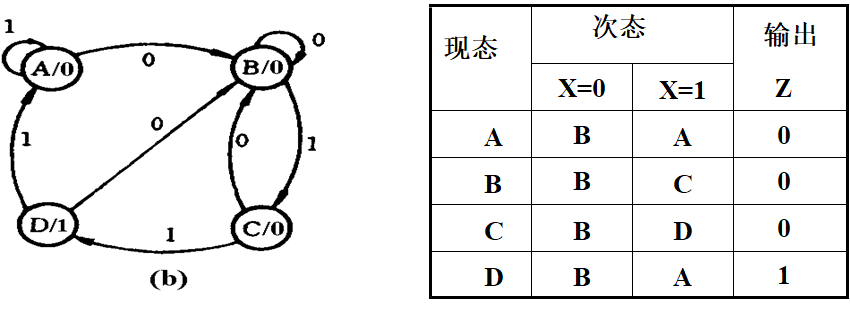
状态化简 ▲
从原始状态表中消去多余状态,得到一个既能正确地描述给定的逻辑功能,又能使所包含的状态数目达到最少的状态表,通常称这种状态表为最小化状态表。
等效状态:如果对于所有可能的输入序列,分别从Si和Sj出发,所得到的输出响应序列完全相同。等效状态具有传递性。
等效条件:满足如下两条。
- 第一,它们的输出相同。
- 第二,它们的次态属于下列情况之一:
- a.次态相同;
- b.次态交错或为各自的现态;
- c.次态循环或为等效对。
最大等效类:如果一个等效类不是任何其他等效类的子集,则该等效类称为最大等效类。
隐含表进行状态化简
例如:
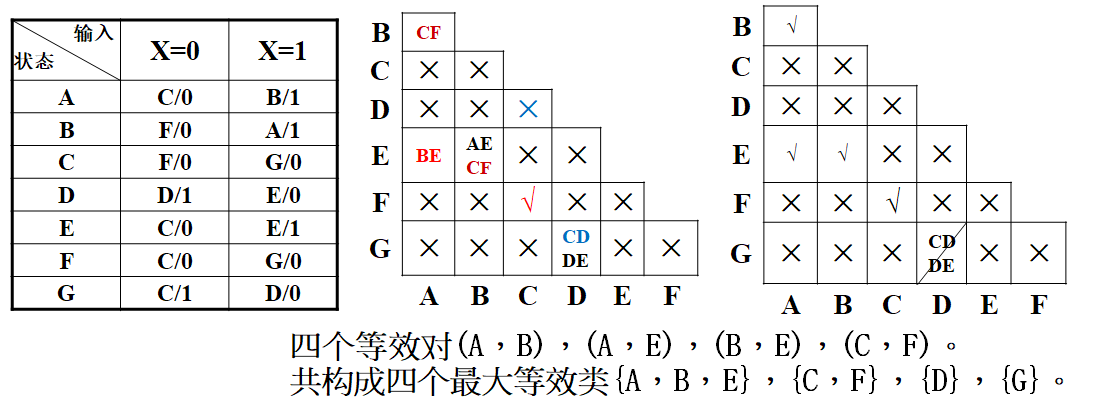
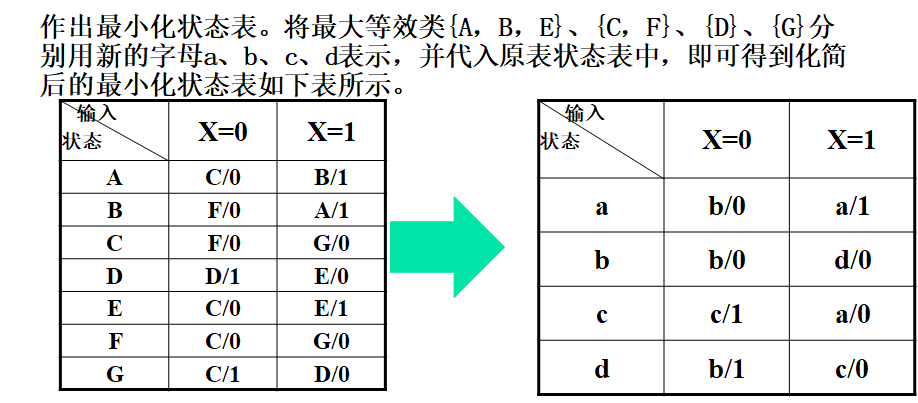
状态编码
相邻法的状态编码原则:按从1至3的优先顺序考虑,一般将初始状态分配为“0”状态。
- 在相同输入条件下,具有相同次态的现态应尽可能分配相邻的二进制代码;
- 在相邻输入条件下,同一现态的次态应尽可能分配相邻的 二进制代码;
- 输出完全相同的现态应尽可能分配相邻的二进制代码。
设计举例
设计一个串行数据检测器。该检测器有一个输入端X,它的功能是对输入信号进行检测。当连续输入三个1(以及三个以上1)时,该电路输出Y=1,否则输出Y=0。
(1)根据设计要求,设定状态:
- S0——初始状态或没有收到1时的状态;
- S1——收到一个1后的状态;
- S2——连续收到两个1后的状态;
- S3——连续收到三个1(以及三个以上1)后的状态。
(2)根据题意可画出原始状态图:

画出原始状态表:

(3)状态化简。观察上图可知,S2和S3是等价状态,所以将S2和S3合并,并用S2表示,得简化状态表: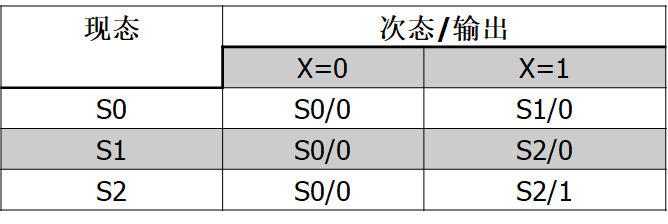
(4)状态分配。该电路有3个状态,可以用2位二进制代码组合(00、01、10、11)中的 三个代码表示。本例取S0=00、S1=01、S2=11。
(5)选择触发器:选用2个D触发器。
(6)求出状态方程、驱动方程和输出方程。
列出D触发器的驱动表、画出电路的次态和输出卡诺图。
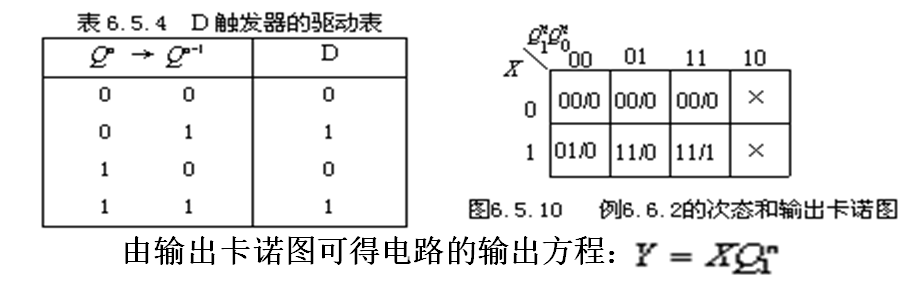
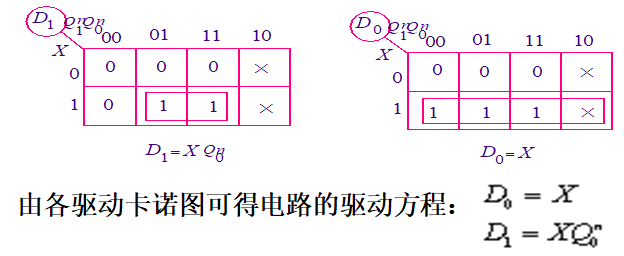
(7)检查能否自启动。
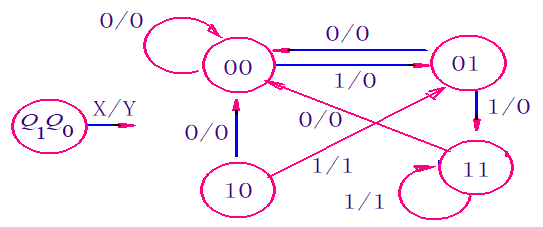
(8)画逻辑图。根据驱动方程和输出方程,画出逻辑图。
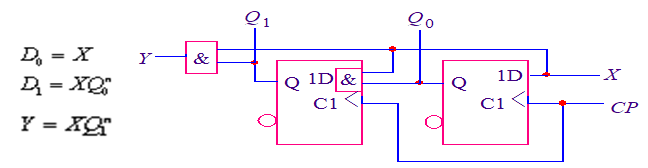
集成电路的应用
计数器
4位同步二进制计数器74161 【重要】:异步清零;同步并行预置数;计数;保持。

十进制计数器74160 【重要】:
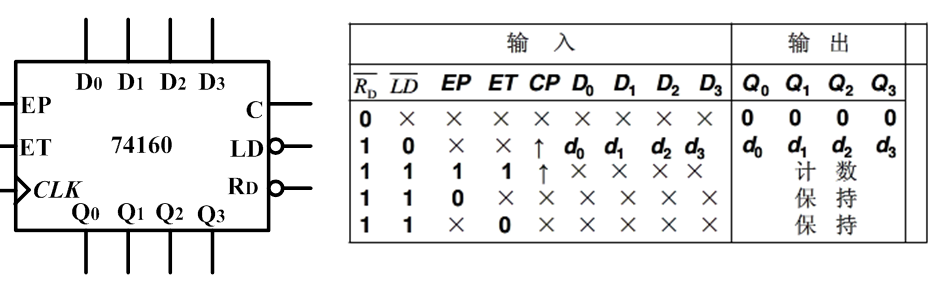
可逆计数器74191:

同步级联
例如:用两片4位二进制加法计数器74161采用同步级联方式构成的8位二进制同步加法计数器,模为16×16=256。
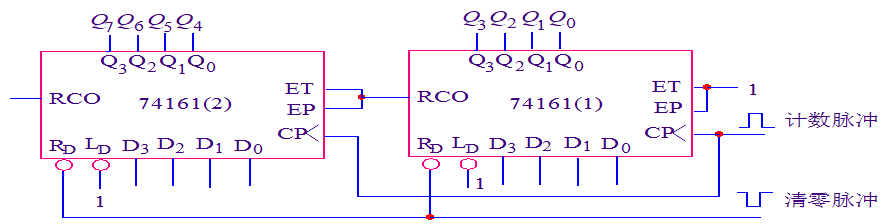
组成任意进制计数器 【重要】
例如:用集成计数器74160和与非门组成的6进制计数器。
异步清零法(RD=Q2Q1)(注意要设计到进位的下一个状态):
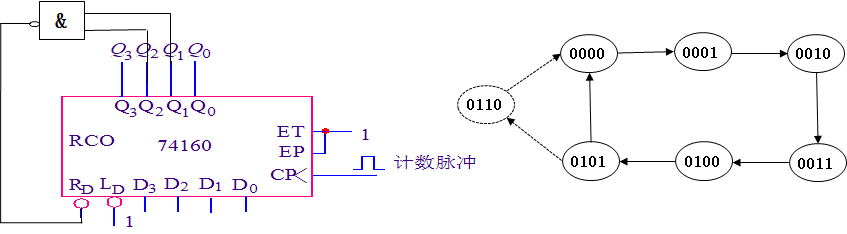
同步置数法(LD=Q2Q0):
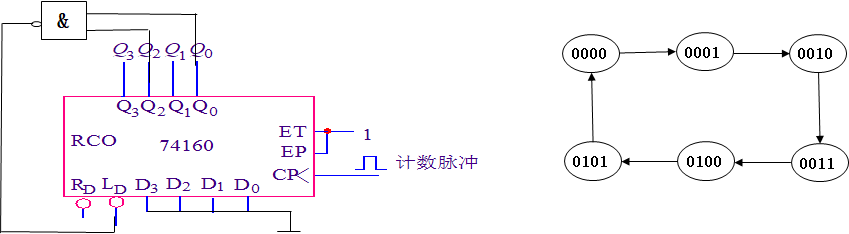
组成序列信号发生器 【重要】
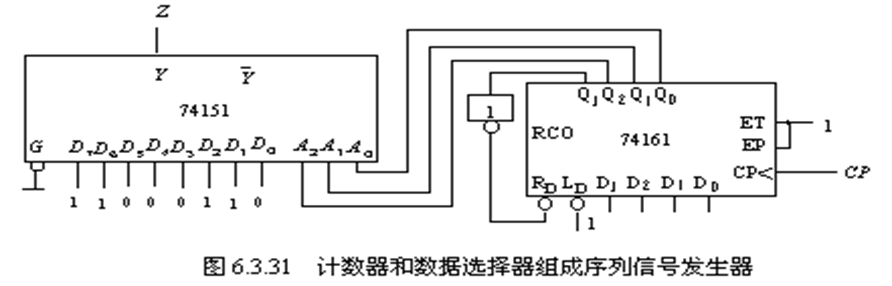
例如:试用计数器74161和数据选择器设计一个01100011序列发生器。
由于序列长度P=8,故将74161构成模8计数器,并选用数据选择器74151产生所需序列,从而得电路如图所示。
寄存器
寄存器:可寄存一组二进制数码的逻辑部件
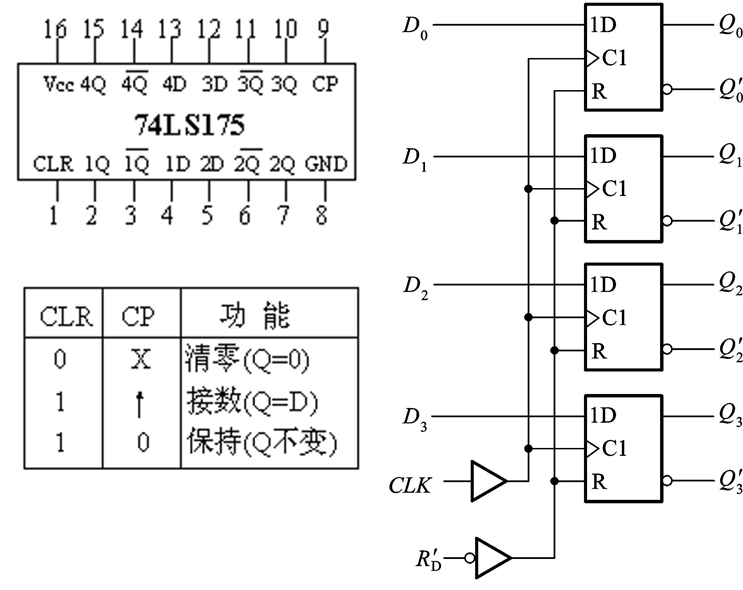
74175为由边沿触发器构成的4位寄存器,为并行输入/并行输出方式。在CLK上升沿时,将D0…D3数据存入;由RD异步清零。
移位寄存器
移位寄存器不仅具有数码存储功能,还具有移位的功能,即在移位脉冲的作用下,依次左移或右移。
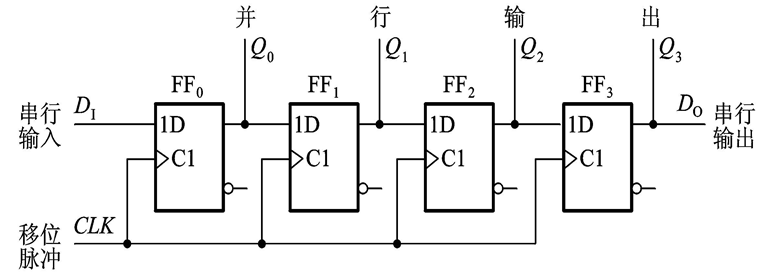
右移寄存器
结构特点:左边触发器的输出端接右邻触发器的输入端。
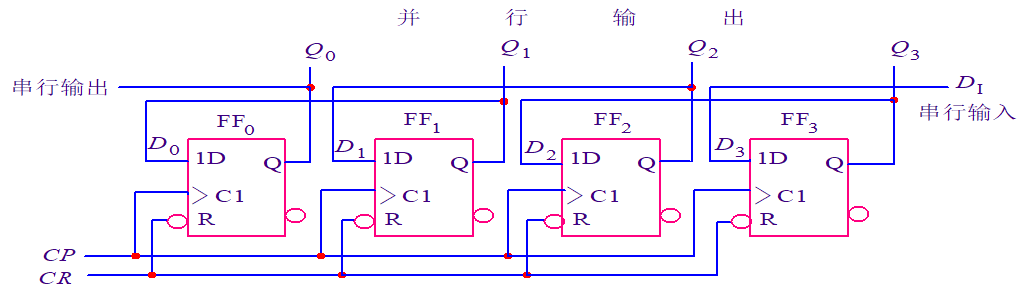
左移寄存器
结构特点:右边触发器的输出端接左邻触发器的输入端。
双向移位寄存器74194 【重要】

- DIR-数据右移串行输入端
- DIL-数据左移串行输入端
- D0…D3-数据并行输入端
- Q0…Q3-数据并行输出端
- S1、S0-工作状态控制端
74194->序列检测器 【重要】
例如:用74194实现“1011”数据检测器
- 待检测序列长度为4,所以选择4位移位寄存器;
- 将待检测序列从状态输出中解读出来(组合逻辑)。

移位寄存器->移位型计数器
- 环形计数器:N位移位寄存器可以计N个数,实现模N计数器。状态为1的输出端的序号等于计数脉冲的个数。
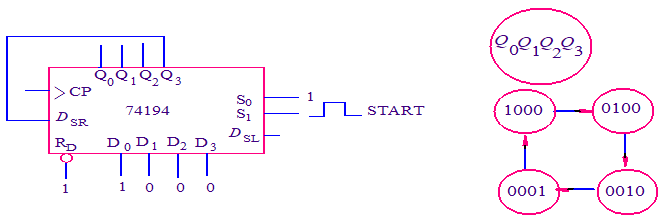
- 扭环形计数器:N位移位寄存器可以组成模2N的扭环形计数器,只需将末级输出反相后,接到串行输入端。

用反馈移位寄存器实现环行计数器的方法:
- 看环行计数器的状态机,是不是具有移位特性
- 选择n位的移位寄存器,并求其反馈函数:反馈函数的输出值其实就是次态串行输入值;
- 通过卡诺图求反馈函数表达式;
- 电路实现。
例如:用194实现3位环行计数器
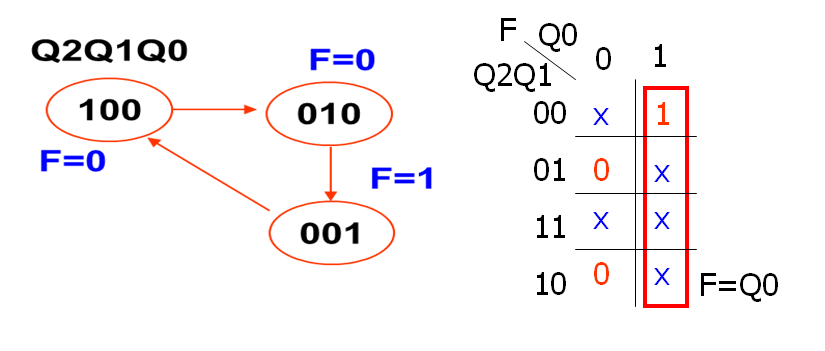
该状态机的移位方向为Q2Q1Q0(右移);其中D2为串行输入端;而Q0为串行输出端。
移位寄存器->序列发生器 【重要】
例如:请用移位寄存器设计一个序列发生器,能够输出串行序列“101110”
步骤一:通过移位特性构建状态图(要求状态图中不能出现重复状态):
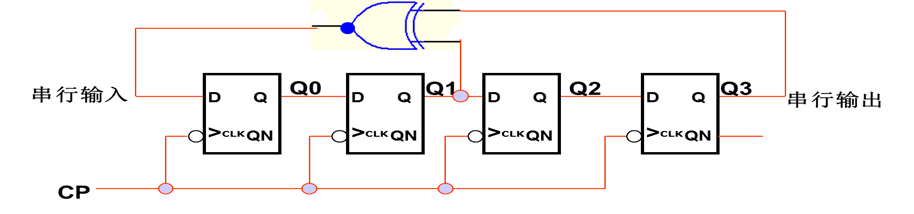
步骤二:上面状态图存在移位特性,根据其移位特性求其反馈函数;Q3为串出;Q0为串入;反馈函数的输出即次态的串入。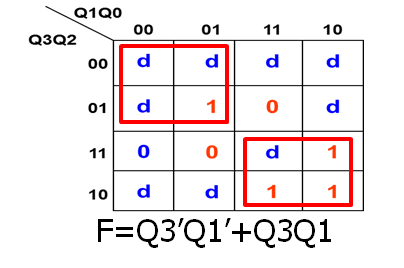
About this Post
This post is written by Holger, licensed under CC BY-NC 4.0.